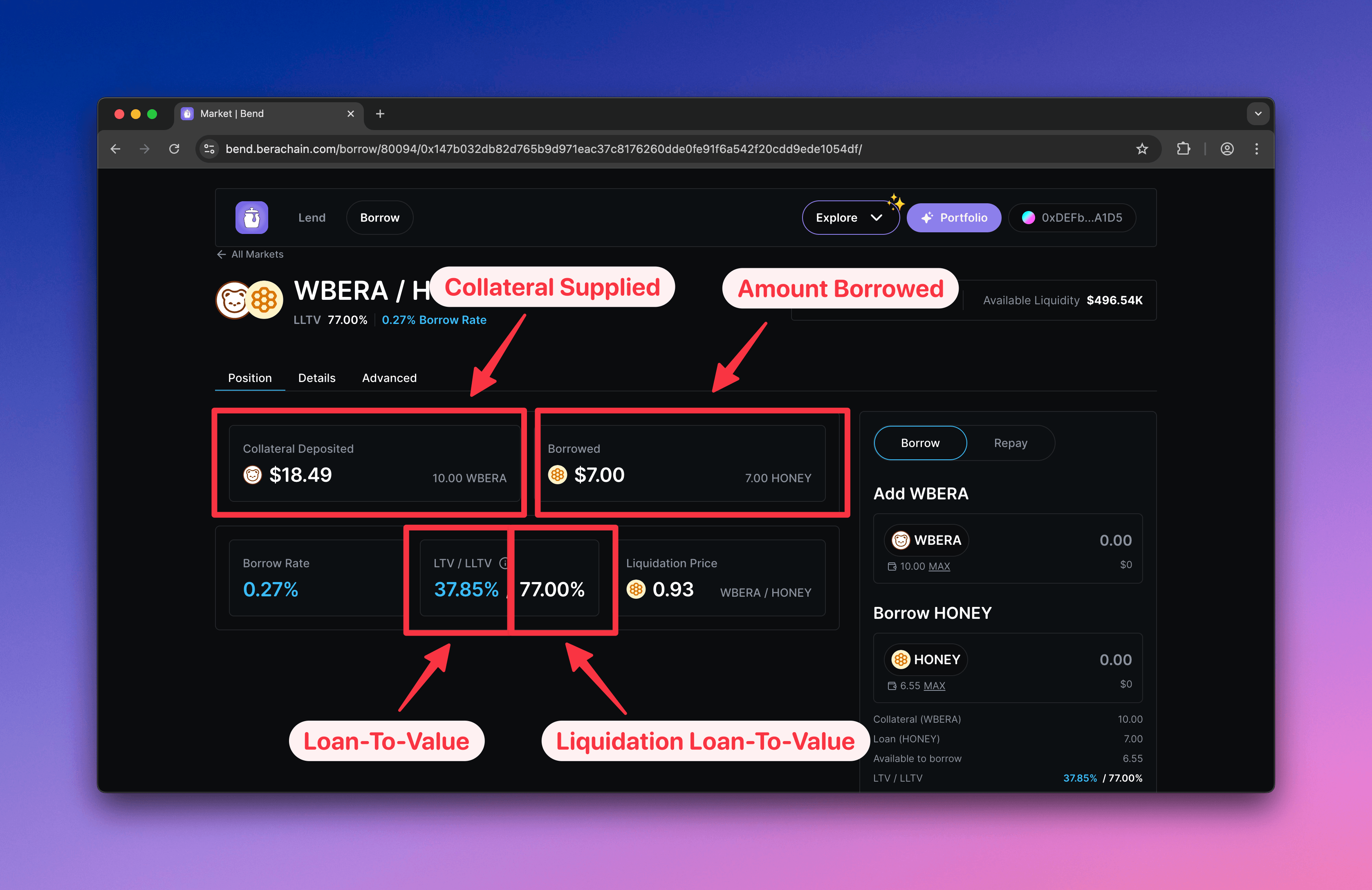
Loan-to-Value (LTV) in Bend

When a user borrows from Bend, their position's safety is determined by the relationship between their collateral, their debt, and the market's risk parameters. Understanding and clearly displaying these metrics is one of the most critical responsibilities when building a lending integration.

Collateral

In Bend, collateral is the asset a user supplies to a lending market to secure their loan. For example, in a $wBERA/$HONEY market, $wBERA is the collateral. This collateral acts as a guarantee for lenders that the protocol can recover funds if the borrower defaults.

A user's collateral is specific to each market; it is not cross-margined at the market level. Also, the action to supply collateral does not generate yield.

Understanding Loan-To-Value (LTV)

It's essential to understand how LTV is calculated and what it represents.

How to Calculate LTV

The Loan-To-Value (LTV) ratio is a key risk metric that measures the proportion of debt relative to collateral value. To calculate the LTV of a position on Bend, use the following formula:

LTV = (BORROWED_AMOUNT / COLLATERAL_VALUE_IN_LOAN_TOKEN) × 100%

Where:

BORROWED_AMOUNT: The amount of borrowed assets of the user (in token base units)
COLLATERAL_VALUE_IN_LOAN_TOKEN: The value of the collateral in terms of the loan token

The collateral value in loan token units is calculated as:

COLLATERAL_VALUE_IN_LOAN_TOKEN = (COLLATERAL_AMOUNT × ORACLE_PRICE) / ORACLE_PRICE_SCALE

Where:

COLLATERAL_AMOUNT: The amount of collateral assets provided by the user (in token base units)
ORACLE_PRICE: The oracle price returned by the oracle of the market (scaled by ORACLE_PRICE_SCALE)
ORACLE_PRICE_SCALE: A scaling factor used by the protocol for price normalization

Liquidation Loan-to-Value (LLTV)

The Liquidation Loan-to-Value (LLTV) is the maximum LTV a position can reach before it becomes eligible for liquidation. It is a fixed, immutable parameter for each market, chosen from a governance-approved list at the time of creation.

The rule is simple and absolute: If LTV ≥ LLTV, the position can be liquidated.

For example, if a market's LLTV is 86%, a user's position is at risk of liquidation as soon as their LTV reaches or exceeds 86%.

Health Factor

The Health Factor is another crucial metric that indicates how close a position is to liquidation:

HEALTH_FACTOR = (COLLATERAL_VALUE_IN_LOAN_TOKEN × LLTV) / BORROWED_AMOUNT

Where:

LLTV: The Liquidation Loan-To-Value threshold set for the market (e.g., 0.86 or 86%), expressed as a WAD (Weighted Arithmetic Decimal - 10^18 scaled value, like 860000000000000000)

A position is healthy when the Health Factor is greater than 1.0. When it falls below 1.0, the position becomes eligible for liquidation.

Example: Calculating LTV and Health Factor

Let's walk through a concrete example of calculating LTV and Health Factor for a position on Bend:

Given values (with assumptions):

Borrowed amount: 150,000 $HONEY (150,000 × 10^18 base units — 18 decimals)
Collateral amount: 2 $WBERA (2 × 10^18 base units — 18 decimals)
Oracle price: 3 $HONEY per $WBERA (value = 3 × 10^18)
Oracle price scale: 10^18
LLTV: 86% (0.86 × 10^18 = 860,000,000,000,000,000 WAD - Weighted Arithmetic Decimal)

Step 1 - Calculate the collateral value in loan token units

The collateral value is 6 $HONEY, meaning the collateral is worth 6 times the price of a single $HONEY unit.

javascript

// All calculations use BigInt for precision
const ORACLE_PRICE_SCALE = 10n ** 18n;

const collateralValueInLoanToken = (collateralAmount * oraclePrice) / ORACLE_PRICE_SCALE;
// = (2n * 10n**18n * 3n * 10n**18n) / 10n**18n
// = 6n * 10n**18n (6 HONEY in base units)

Step 2 - Calculate the current LTV

javascript

const WAD = 10n ** 18n;

const borrowedAmount = 150_000n * 10n ** 18n; // 150,000 HONEY
const collateralValueInLoanToken = 6n * 10n ** 18n; // 6 HONEY equivalent (scaled)

const currentLTV = (borrowedAmount * WAD) / collateralValueInLoanToken;
// = (150,000 * 10^18 * 10^18) / (6 * 10^18)
// = 25,000 * 10^18 (representing 25000% or 250x over-collateralized, unrealistic example for illustration)

For a realistic example, let’s assume instead:

Borrowed amount: 150 $HONEY (150 × 10^18)
Collateral: 2 $WBERA (worth 6 $HONEY)

javascript

const borrowedAmount = 150n * 10n ** 18n; // 150 HONEY
const collateralValueInLoanToken = 6n * 10n ** 18n; // 6 HONEY equivalent

const currentLTV = (borrowedAmount * WAD) / collateralValueInLoanToken;
// = (150 * 10^18 * 10^18) / (6 * 10^18)
// = 25 * 10^18 (2,500%)

This means the position is massively over-leveraged, so the Health Factor will be far below 1.0.

Step 3 - Calculate the health factor

javascript

const lltv = 86n * 10n ** 16n; // 0.86 scaled to WAD

const healthFactor = (collateralValueInLoanToken * lltv) / borrowedAmount;
// = (6 * 10^18 * 0.86 * 10^18) / (150 * 10^18)
// = 0.0344 * 10^18 (scaled by WAD)

const healthFactorDisplay = Number(healthFactor) / Number(WAD);
// = 0.0344

The Health Factor of 0.0344 means this position is deeply undercollateralized and subject to immediate liquidation.

Step 4: Adjusting for a Healthy Position

Let’s correct the values for a more reasonable example:

Borrowed amount: 150 $HONEY (150 × 10^18)
Collateral: 100 $WBERA (worth 300 $HONEY)

javascript

const borrowedAmount = 150n * 10n ** 18n;
const collateralValueInLoanToken = 300n * 10n ** 18n;
const lltv = 86n * 10n ** 16n;

const healthFactor = (collateralValueInLoanToken * lltv) / borrowedAmount;
// = (300 * 10^18 * 0.86 * 10^18) / (150 * 10^18)
// = 1.72 * 10^18 (scaled)

const healthFactorDisplay = Number(healthFactor) / Number(WAD);
// = 1.72

Since the Health Factor = 1.72, this position is healthy, with a 72% safety margin before liquidation.

Summary of Position:

Metric	Value
Current LTV	50.00%
Max LTV (LLTV)	86.00%
Health Factor	1.72
Status	✅ Healthy
Liquidation Buffer	36.00%

This demonstrates how $WBERA (18 decimals, priced at 3 $HONEY each) serves as collateral against a $HONEY (18 decimals) loan, using standardized WAD scaling for precise on-chain computation.

The Role of Oracles

The accuracy of LTV and Health Factor calculations depends on the Oracle Price.

Dynamic Pricing: The oracle provides the real-time exchange rate between the collateral and loan assets. This price is the most dynamic variable in the health calculation.
Oracle Complexity: The oracle for a market might not be a single price feed. It could be a combination of feeds or rely on other onchain data.
Risk Exposure: The reliability of your LTV and Health Factor display is a direct reflection of the oracle's reliability. Any latency, inaccuracy, or manipulation of the oracle's price can directly impact user positions.

When displaying market information, it is crucial to also provide transparency about the oracle being used.

If you'd like to learn more about the oracles, see Bend Oracle.

Loan-to-Value (LTV) in Bend ​

Collateral ​

Understanding Loan-To-Value (LTV) ​

How to Calculate LTV ​

Liquidation Loan-to-Value (LLTV) ​

Health Factor ​

Example: Calculating LTV and Health Factor ​

Step 1 - Calculate the collateral value in loan token units ​

Step 2 - Calculate the current LTV ​

Step 3 - Calculate the health factor ​

Step 4: Adjusting for a Healthy Position ​

Summary of Position: ​

The Role of Oracles ​

Loan-to-Value (LTV) in Bend

Collateral

Understanding Loan-To-Value (LTV)

How to Calculate LTV

Liquidation Loan-to-Value (LLTV)

Health Factor

Example: Calculating LTV and Health Factor

Step 1 - Calculate the collateral value in loan token units

Step 2 - Calculate the current LTV

Step 3 - Calculate the health factor

Step 4: Adjusting for a Healthy Position

Summary of Position:

The Role of Oracles