Interest Rate Model

Here is an example video showing how the Adaptive Curve IRM works:

Video provided by Morpho Docs.

In Bend, the interest rate borrowers pay is determined by an external Interest Rate Model (IRM), which is selected at the time each market is created.

Currently, the only IRM available for Bend markets is the AdaptiveCurveIRM. This model stands apart from traditional lending pool IRMs in two main ways:

1. Whereas most lending pool IRMs can be changed or upgraded, the AdaptiveCurveIRM is immutable and cannot be altered. As a result, it must automatically respond to market conditions, including shifts in interest rates across other platforms.

2. In the Bend protocol, supplied assets are not used as collateral. This means markets do not need to maintain excessive liquidity for potential liquidations at all times. By eliminating this risk, the protocol can target a higher utilization of capital and impose less severe penalties for illiquidity, which leads to improved market efficiency.

The AdaptiveCurveIRM mechanism is built to keep utilization near its target—set at 90%. There are two overlapping timeframes: in the short-term, the protocol seeks to avoid utilization becoming too low or too high (to prevent liquidity disruptions), while over the medium and long term, the rate adapts to ongoing market changes.

To maintain this balance, AdaptiveCurveIRM modifies incentives for users through two main mechanisms:

• The Curve Mechanism
• The Adaptive Mechanism

The Curve Mechanism

This mechanism resembles the interest rate curves commonly found in traditional lending protocols.

The curve is defined by the following features:

Name	Description
Target Rate	$r_{90\mathrm{\%}}$ (corresponding to a target utilization of 0.9)
Fixed Steepness Parameters	c = 4

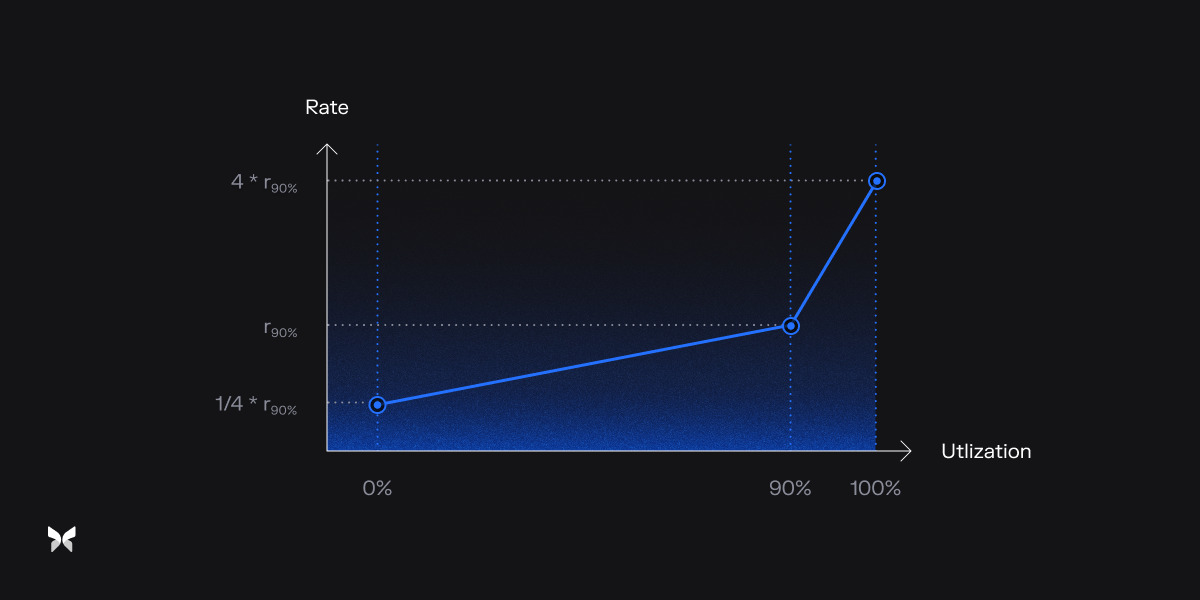
Image provided by Morpho Docs

Each time a user interacts with the market—such as borrowing or repaying—the utilization changes. This causes an immediate, stepwise shift in the rate as set by the curve.

For instance, the following are sample utilization-to-rate relationships:

Utilization	Rate
90%	$r_{90\mathrm{\%}}$
100%	$4\times r_{90\mathrm{\%}}$

The Curve Mechanism is designed to respond to short-term fluctuations in utilization, helping maintain healthy market liquidity during periods of sudden borrowing or repayment.

The Adaptive Mechanism

This mechanism continuously shifts the curve to adjust to market conditions over time.

Importantly, the interest rate adapts along with the curve itself, so it continually evolves based on market conditions—even in periods without any market activity.

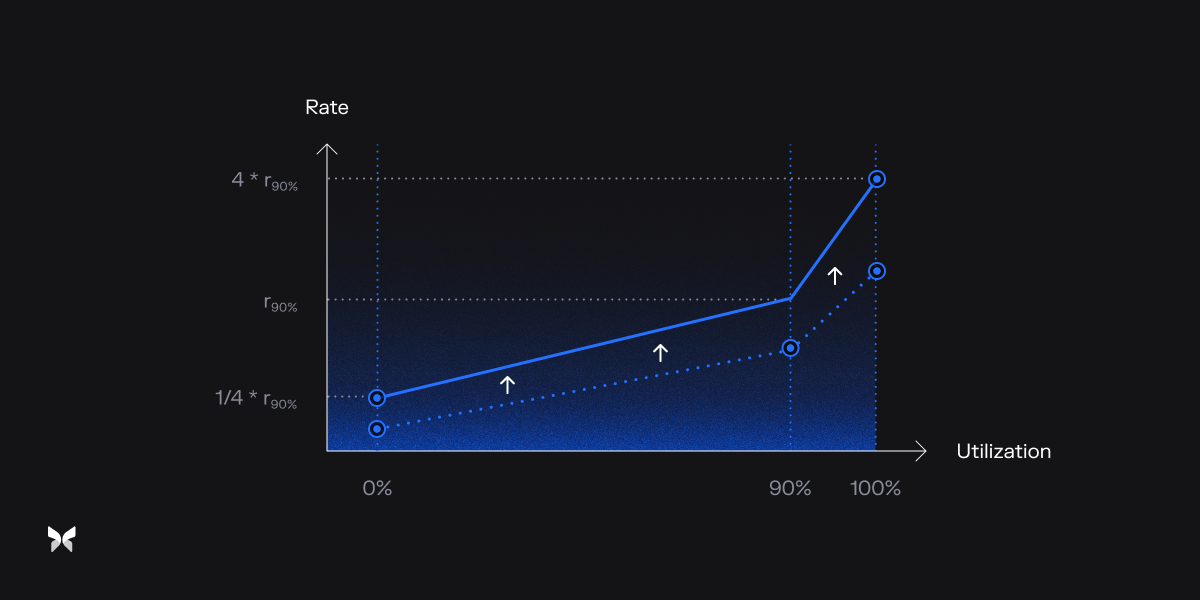
Image provided by Morpho Docs

The adaptive mechanism dynamically shifts the rate curve in response to changing market conditions, even during periods without user interaction.

The key value that moves the curve is $r_{90\mathrm{\%}}$—the rate at the target utilization. This value gradually changes over time:

• If utilization rises above the target (90%), $r_{90\mathrm{\%}}$ will steadily increase.
• If utilization falls below the target, $r_{90\mathrm{\%}}$ will steadily decrease.

The pace at which $r_{90\mathrm{\%}}$ moves is recalculated whenever the market is updated (such as through borrowing or repaying). The greater the gap between current and target utilization, the faster $r_{90\mathrm{\%}}$ (and thus the whole curve) moves in the appropriate direction.

As an example: if utilization holds steady at 100% for five days, $r_{90\mathrm{\%}}$ will, at maximum speed, approximately double over that time period.

TIP

The values of some constants are hardcoded into the code deployed on Berachain, such as TARGET_UTILIZATION, INITIAL_RATE_AT_TARGET, etc.

Formula Breakdown

Name	Description
$u$	utilization - total assets borrowed divided by total assets supplied
$t$	time - the specific moment at which utilization and other parameters are evaluated
$u(t)$	Ratio of total borrow over total supply at time
$u_{\text{target}}=0.9$	Constant target value for utilization (set to 0.9) that the model aims to maintain.
$\forall t$	For all time
$e$	error - Difference between the current utilization and the target utilization, divided by a normalization factor
$k_{\text{d}}$	Constant that controls how sharply the interest rate increases when utilization exceeds the target
$H$	The time step (in seconds) between two interest rate updates
$last$	Most recent interaction time before or at a specific time
$speed(t)$	Factor controlling how quickly the interest rate evolves based on utilization changes over time
$r$	Borrow rate
$r_{\text{T}}$	Rate at target - Interest rate corresponding to the target utilization, updated over time using the speed factors

Utilization

Utilization ($u(t)$) is the ratio of total borrowed assets to total supplied assets at time ($t$), with a constant utilization target ($u_{\text{target}}=0.9)$.

Error

Error ($e(u)$) is the normalized difference between the current utilization ($u(t)$) and the target utilization ($u_{\text{target}}$), scaled so that the distance between $u_{\text{target}}$ and $u=1$ equals the distance between $u_{\text{target}}$ and $u=0$.

$$\mathrm{\forall }t,e(u)=\{\begin{array}{ll}{\displaystyle \frac{u(t)-u_{\text{target}}}{1-u_{\text{target}}}},& \text{if }u(t)>u_{\text{target}}\\ {\displaystyle \frac{u(t)-u_{\text{target}}}{u_{\text{target}}}},& \text{if }u(t)\le u_{\text{target}}\end{array}$$

Image provided by Morpho Docs

Curve

Curve ($curve(u)$) determines the shape and sensitivity of the interest rate response to changes in utilization around the target, with different slopes below and above $u_{\text{target}}$ controlled by the constant $k_{\text{d}}$.

$$\text{curve}(u)=\{\begin{array}{ll}(1-{\displaystyle \frac{1}{k_d}})\cdot e(u)+1,& \text{if }u\le u_{\text{target}}\\ (k_d-1)\cdot e(u)+1,& \text{if }u>u_{\text{target}}\end{array}$$

with

$$k_d=4$$

History Of Interactions

History of interactions ($H$) represents the set of all past interaction times up to time ($t$), including the initial time ($0$). Noting that $t_{\text{i}}$ the time at which $i\text{th}$ interaction occured.

$$\mathrm{\forall }t,H(t)=\{0\}+\{t_i{\}}_{t_i<t}$$

Last Interaction

Last interaction ($last$) represents the most recent interaction time before or at time ($t$).

$$\mathrm{\forall }t,\text{last}(t)=max(H(t))$$

Speed

Speed factor ($speed$) determines how fast the interest rate changes over time based on the error at the last interaction, scaled by ( $k_{\text{p}}$ ).

$$\mathrm{\forall }t,\text{speed}(t)=\exp (k_p\cdot e(u(\text{last}(t)))\cdot (t-\text{last}(t))),\text{with }{k}_p=50$$

Rate At Target

Rate at target ($r_{\text{target}}$) represents the interest rate when utilization equals the target utilization, evolving over time based on the speed factor.

$$\mathrm{\forall }t>0,r_T(t)=r_T(\text{last}(t))\cdot \text{speed}(t)$$

At any time ($t$), the borrow rate ($r$) is given by the formula:

$$r(t)=r_T(t)\cdot \text{curve}(u(t))$$

Calculations

Annual Percentage Yield (APY) is a standardized metric that expresses the annualized return for suppliers and the annualized cost for borrowers, accounting for the effects of compounding interest over a one-year period. In Bend, APY enables participants to directly compare returns and costs across different protocols and asset markets.

Borrow APY

The Borrow APY is calculated using the following formula:

$$\text{borrowAPY}=(e^{(\text{borrowRate}\times \text{secondsPerYear})}-1)$$

Where:

• borrowRate is the borrow rate per second, as determined by the Interest Rate Model (IRM).
• secondsPerYear represents the total number of seconds in a year (31,536,000).

Supply APY

The Supply APY is calculated considering the utilization and the fee. The formula is:

$$\text{supplyAPY}=\text{borrowAPY}\times \text{utilization}\times (1-\text{fee})$$

Where:

• fee is the fee of the market on a per-market basis and portion of the interest paid by borrowers that is retained by the protocol. See Yield & Fees for more details.
• utilization is calculated as:

$$\text{utilization}=\frac{\text{totalBorrowAssets}}{\text{totalSupplyAssets}}$$

Constants

The values of the following constants are hardcoded into the Morpho code deployed on Berachain.

• WAD = Wei-based Decimal (WAD = 10¹⁸, meaning 1 WAD = 1.0)

Parameter	Description	Value
CURVE_STEEPNESS	Curve steepness (scaled by WAD)	4
ADJUSTMENT_SPEED	Adjustment speed per second (scaled by WAD)	50/# of seconds per year
TARGET_UTILIZATION	Target utilization (scaled by WAD)	90%
INITIAL_RATE_AT_TARGET	Initial rate at target per second (scaled by WAD)	4%/# of seconds per year
MIN_RATE_AT_TARGET	Minimum rate at target per second (scaled by WAD)	0.1%/# of seconds per year
MAX_RATE_AT_TARGET	Maximum rate at target per second (scaled by WAD)	200%/# of seconds per year